一些量子计算的东西
前几天看到一个有趣的东西,这篇文章在尝试寻找大脑用了某些量子相关的东西的证据。大概就是用已知的量子系统去干涉未知系统,如果两个系统成功发生了纠缠,就可以认为未知系统是非经典的。这就比较有意思了,某种程度上来说给了人工神经网络启发。
那就总结一下,量子力学以及量子计算咯
观前提示:本文假设您有线性代数,概率论和物理学高中水平。
粒子
反正课本里都学了,再写一遍也没啥坏处
基本相互作用
宇宙中粒子可以互相影响
强相互作用
最强并且第二短的作用力,作用与强子之间,质子和中子之间的核力就算。夸克模型里胶子负责传递强相互作用。
弱相互作用
最短并且很弱的作用力,在费米子之间。由W及Z玻色子的交换引起。
电磁相互作用
电场和磁场带来的力。与粒子固有的电荷和自旋属性有关。电荷产生电场,而运动的电场产生磁场(磁力是在不同参照系下用于保持电磁力恒定所产生的)。
引力相互作用
就是引力,然而引力子还没被实验确认。与粒子的质量有关。
量子力学中的粒子
费米子
费米子遵循费米-狄拉克统计,包括所有的夸克和轻子。自旋为半奇数。
费米子的波函数反对称,因此交换两个费米子之后波函数会反过来。所以费米子遵循泡利不相容,即两个全同的费米子不能拥有相同的量子态。这样在相同轨道的电子必须有相反的自旋。
玻色子
玻色子遵循玻色-爱因斯坦统计。玻色子包含光子,胶子,W和Z玻色子。
玻色子的波函数对称,因此交换两个玻色子后波函数并不会改变。
自旋为整数的粒子是玻色子,自旋为半整数的粒子是费米子。
原子 (Atom)
基本上,原子都是由一个原子核和外面的电子组成。原子核带正电,而电子都带负电。
原子轨道 (Atomic orbital)
这玩意描述电子在原子核外面某个位置找到它们的可能性。其实并不是轨道,而是概率分布。
电子都被锁在离散的能级(Energy level)上,而这些能级赋予了电子势能(负的)。电子可以通过吸收外部能量跑到不同的高能级,也会自发性的坠回低能级并放出能量(通常是光子)。
因为泡利不相容原理,同一个轨道上都可以有两个自旋相反的电子。
量子
参与物理作用实体的最小量,都是很小很小的微观粒子。因为在如此小的情况下,它们的行为已经无法用经典力学来描述了。只能引入新的词汇来描述它。
测不准原理 (Uncertainty principle)
因为我们是世界的一部分,所以任何对世界的测量都会对世界造成影响。这种影响无法被消除。
例,我们要测量一个粒子,普遍的方法是用光子去撞击然后看反弹。
光子的能量与波长成反比,而光子的能量会被传递给粒子从而改变它的动量。
波长越小我们获得粒子的位置越精确,而改变粒子动量越多则获得它的动量越不精确。
同样,波长越大我们获得粒子的位置越模糊,而改变粒子动量越少则获得它的动量越精确。
这是鱼与熊掌不可兼得的事实。我们只能要么知道粒子精确的位置要么知道精确的动量。
自旋
大概科学家们发现在畸变磁场中,即使电子没在运动,它也会收到某种力。这说明电子自己也在产生磁场。
额,所以它在转吗?我们也没办法知道,所以干脆把它变成这些玩意自身的属性之一:自旋(Spin)。
自旋的大小是粒子们与生俱来的属性。但是自旋的方向嘛,随便改咯。
大粒子自旋可以由它下面小粒子的自旋相加得到。
对于量子来说,它的基本属性就是:自旋,质量和电荷
自旋会创造磁场,内部磁感线方向与自旋方向相同。所以箭头指向S极。
波函数 (Wave function)
波函数用来描述一个量子的状态,是一个概率密度函数。薛定谔方程可以描述它如何随着时间变化。
在量子世界里,万物皆是概率。
波函数叠加 (Superposition)
本征态(纯态)
进行了测量之后,所有的量子态都会变成本征态,而概率幅决定了我们测量到不同本征态的概率
叠加态
叠加态为不同本征态之间的线性组合。如果$a_1$和$a_2$是两个不同的本征态,$c_1$和$c_2$是它们的概率幅,则它们的叠加态为。
$|\psi\rangle=c_{1}|a_1\rangle+c_{2}|a_2\rangle$
量子系统都可以处于叠加态
波函数坍缩 (Collapse of wave function)
对量子进行测量时其状态立马从叠加态变成本征态的过程。
量子纠缠 (Entanglement)
来自同一个粒子变成的两个粒子,它们两个状态的叠加等于原先粒子的状态。这就意味着两个粒子的状态是反关联的。
而这样神奇的是,当测量了其中一个粒子,两边的波函数会同时坍缩,从叠加态变为一个本征态,则由于以上的性质,如果我们测量另一个粒子则它会呈现相反的另一个本征态。
量子隧穿
由于量子的位置是由波函数这样一个概率函数描述的,所以在很靠近一个有限位势垒时候,就有很大概率粒子可以出现在它的对面,看起来就像粒子无需跨过比它高的能量壁垒直接过去了一样。
量子计算
数学
有了以上关于量子系统的性质描述,我们可以构建理想量子系统的数学模型。
在量子计算中,与传统计算的二进制bit不一样,它用qubit。qubit = quantum+bit,所以是由量子来表示状态,一般用自旋方向表示状态。
布洛赫球面 (Bloch sphere)
我们可以把量子的自旋可能的方向看成一个球,而bloch sphere就是专门为量子纯态建模的
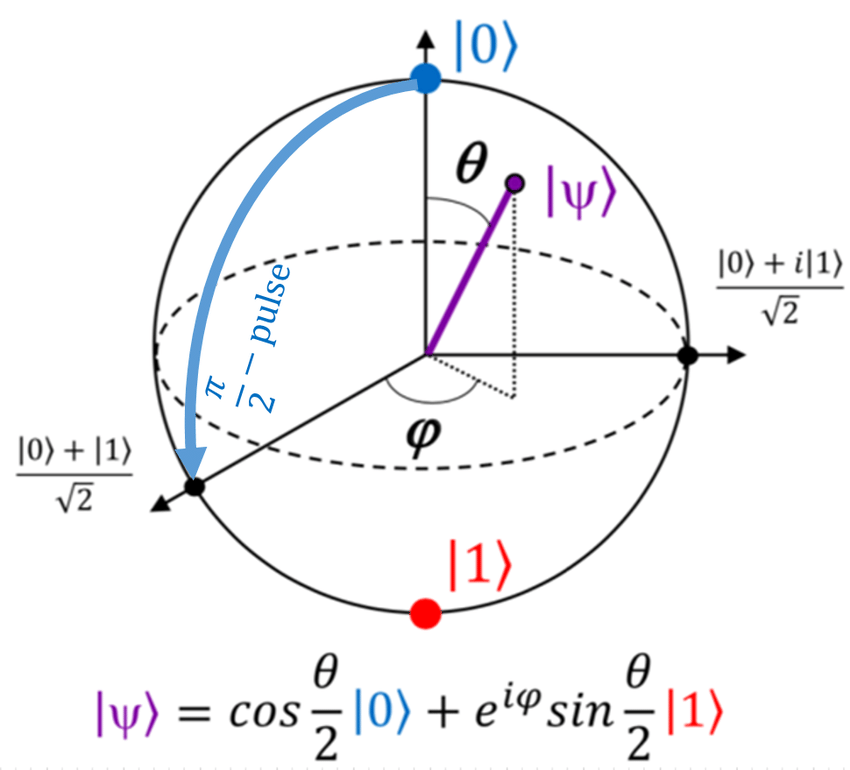
最上面和最下面代表的是两个本征态,$|0\rangle$ 和 $|1\rangle$。而转动到中间的位置就是它们的叠加态。怎么样,是不是挺形象的。
而这个x轴和y轴告诉我们,这两个本征态的组合用到的系数是复数。
我们现在得到的叠加态是
$|\psi\rangle=a_{0}|0\rangle+a_{1}|1\rangle$
其中 $a_0$ 和 $a_1$ 都是复数 $x + iy$ 这样的
而这个球的模型告诉我们为了让其成立,$\sqrt{|a_0|^2 + |a_1|^2} = 1$,要不然叠加超出去了。具体为什么可以去详细瞭解 Born rule。
当我们测量它的时候,它会随机坍缩成两个本征态。而它们的概率取决于这两个系数的平方,即
$P( |0\rangle ) = |a_0|^2$
$P( |1\rangle ) = |a_1|^2$
来到传统的概率学是不是挺熟悉了)
由此可见,这玩意最牛逼的在于每个量子比特实际上给你存了两个复数进去!
来点线代
对于这些状态,我们可以写成矩阵方便计算
本征态0可以表示为
$$
|0\rangle =
\begin{bmatrix} 1 \ 0 \end{bmatrix}
$$
本征态1可以表示为
$$
|1\rangle =
\begin{bmatrix} 0 \ 1 \end{bmatrix}
$$
它们的线性组合也就是qubit的状态为
$$
|\psi\rangle =
a_0 \begin{bmatrix} 1 \ 0 \end{bmatrix} +
a_1 \begin{bmatrix} 0 \ 1 \end{bmatrix} =
\begin{bmatrix} a_0 \ a_1 \end{bmatrix}
$$
并且 $a_0, a_1 \in \mathbb{C}$。
因为我们想让 $|||\psi\rangle||_z = 1$,所以才得出$\sqrt{|a_0|^2 + |a_1|^2} = 1$
很正常,概率相加等于1。
多比特测量
当我们有两个量子比特,可以这么写它们总的叠加态
$|\psi\rangle=a|00\rangle+b|01\rangle+c|10\rangle+d|11\rangle$
更多的也可以再往上写。
而这个符号里有两个数字在,其实是张量乘法(Tensor product)的缩写。
$|\psi\rangle \otimes |\psi^{\prime}\rangle = |\psi\rangle|\psi^{\prime}\rangle = |\psi\psi^{\prime}\rangle$
它的定义为
$\begin{bmatrix} a_0 \ a_1 \end{bmatrix} \otimes \begin{bmatrix} b_0 \ b_1 \end{bmatrix} = \begin{bmatrix} a_0b_0 \ a_0b_1 \ a_1b_0 \ a_1b_1 \end{bmatrix}$
所以对于这几个量子比特的组合,就是
$|00\rangle = \begin{bmatrix} 1 \ 0 \ 0 \ 0 \end{bmatrix}$
$|01\rangle = \begin{bmatrix} 0 \ 1 \ 0 \ 0 \end{bmatrix}$
$|10\rangle = \begin{bmatrix} 0 \ 0 \ 1 \ 0 \end{bmatrix}$
$|11\rangle = \begin{bmatrix} 0 \ 0 \ 0 \ 1 \end{bmatrix}$
看起来就是把二进制表示成为了One-Hot编码。
如果我们测量这两个量子比特,那么获取到 $|00\rangle$ 的概率很显然就是它系数的平方 $|a|^2$。
但是在这种表示方法下,如果我们只测量第一个量子比特,那么获取到 0 的可能性有两组: $|00\rangle$ 和 $|01\rangle$ ,所以这时候的概率为它们俩平方和 $|a|^2 + |b|^2$。
我们可以把这种多比特的表示方法和单比特之间进行转换(如果只考虑其中一个比特)。
对于第一个比特那就是$(\sqrt{|a|^2+|b|^2})|0\rangle + (\sqrt{|c|^2+|d|^2})|1\rangle$
但是为什么我们要写出这种多比特形式呢?
第一是因为,每个量子比特之间的状态互不干扰,是统计学上独立的。所以二维向量就不太够,必须用更高维度的向量来表示所有bits。
第二是因为,多个量子比特会引入新的状态:纠缠态(Entangled state)。
纠缠态不能用简单的张量积来表示,必须用不同量子比特状态的叠加来表示。
考虑这种情况,因为是做了加法,它的结果还是处在可行的张量积空间内。
$|\phi\rangle^{+} = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)$
在这种状态下我们发现,获得 $|00\rangle$ 和 $|11\rangle$ 结果的概率相等,这也就意味着两个量子比特的状态已经绑定了,成为了纠缠态。
如果我们想使用张量积来表示,会发现根本不存在这种情况。具体推导可以自己试试?
混合状态 (Mixed state)
上面考虑的过于理想,在实际的量子计算机中,我们不可避免会引入外部噪声。
量子退相干 就可以改变它的状态,因为量子系统没办法完全与外界隔绝,导致随着时间的迁移外部状态渐渐对内部造成很大影响。
所以上面的理想情况下的量子态 $|\psi\rangle$ 我们称为纯粹的量子态 (pure)
接下来我们需要一个新的数学工具来更好的表示新的混合态:密度矩阵 (Density matrix)。
密度矩阵可以让我们处理有纠缠态和有噪声的情况。
未完待续