Pixivel 这个项目,大概已经存在了三年甚至四年之久了。这是我唯一一个维护的大型网站(对我来说),也是凝聚了我们众多心血的地方。在此期间,她经历了三次版本大改,无数次的增量迭代。现在的后端和前端系统,我敢说已经十分的健壮,并且已经积累了惊人的用户量。
目前的新v2后端架构,整体为持久化爬虫架构。也就是说,我们将原站pixiv的所有插画元数据都在本地数据库保存一份。这样,我们便拥有了甚至在原站下线,依然可以提供服务的能力。
所以,请求原站的推荐接口实在是违背这一套自治系统的准则。有没有办法,可以让我们用数据库本地的信息,生成对应的推荐呢?
答案自不必多说,Pixivel 新版的存在就是最好的证明。
问题分析
首先呢,我们需要给任意一张数据库中的插画,提供对应的相似推荐。就比如你点开初音未来的一张图,下面的推荐应该就是一堆初音未来的图,甚至雪初音都可以被推出来。
这里呢,我们需要一个度量标准来计算两张插画的匹配度。那么我们列出所有的元数据来看看:
- 每个插画独特的id
- 长宽
- 作者
- 标题
- 简介
- 标签
- 图片链接
这里仔细想想,会发现有这么几种方法:
- 同一个作者画的画可能相关度比较高
- 图片自身内容相吻合的画相似度高
- 如果一个人看了这张图并点赞,同时他也喜欢看别的图,那么就认为这些图相似度高。
- 标签差不多的图相似度高
对于第一种的话,经过详细论证发现并不是这样。对于同一个作者来说,画的内容有可能很相似,也有可能大相径庭。
第二种的话,确实是有道理,但是光凭机器本身并不好判定图片的内容。比较靠谱的办法是用监督学习来给图片贴标签,但是这样一来,图片自己带的标签就会???
第三种的话,比较接近目前各大公司采用的推荐系统了。这些通过用户行为分析,经过神经网络进入数据库的特征,已经证明有很好的推荐能力。但是我决定目前并不采用,原因如下
- 需要很牛逼的神经网络模型和数据库才能支撑得起。双塔推荐模型都有点过时了。更别说我这样的小团队运营的站点,自己研发神经网络?不可能。买那么多牛逼的服务器?也不可能。我又不是做淘宝去了,还管什么推荐系统几步曲,什么粗排精排吗?
- 用户隐私是很重要的问题。有可能你觉得这个没什么,不算隐私。但是对于我来说,任何用户数据的泄露都是很严重的事情,编写隐私政策也是很麻烦的事情(虽然不得不做)。我不能负担得起让用户把行为日志交给我的责任。
最后,我们很容易发现,最后一种方法的可操作性,经济性以及实用性角度来说,都是一个理想的选择。不如选它咯。
算法设计
首先,对于每个图片来说,都有一组标签来标识这个图片的类别。这些标签是由创作者贴上去,并且经过筛选的,所以真实度可以保证。
我们可以将一组标签看作是一个集合:
$T = {tag_1, tag_2, tag_3, .... , tag_n}$
而我们需要的,正是两个标签集合的相似度,即为标签的匹配程度。标签重复越多,则越匹配,越该被推荐。
于是我们采用 Jaccard Similarity 计算集合的相似度:
$Jaccard(A, B) = \frac{\left|A\cap B\right|}{\left|A\cup B\right|}$
两个集合交集的大小比上它们并集的大小就是相似度,听起来确实很有道理。
这样就很简单的实现了图片推荐?不,难的在后面。
这样的写法只能成为单独比较,不支持快速查询,只能暴力搜索。把数据库里所有集合都拿出来比一遍。这河里吗?
为此,我们需要先引入一个新的概率搜索方式:MinHash 和 LSH
MinHash
假设现在我们有四个集合 A, B, C, D,并且这四个集合都有一些元素,$A = {a, b}$, $B = {c, d, e}$, $C = {a, d, e}$, $D = {a, b, d}$。它们的并集为$U = {a, b, c, d, e}$。通过0-1编码,我们可以得到如下矩阵:
| Element | A | B | C | D |
|---|---|---|---|---|
| a | 1 | 0 | 1 | 1 |
| b | 1 | 0 | 0 | 1 |
| c | 0 | 1 | 0 | 0 |
| d | 0 | 1 | 1 | 1 |
| e | 0 | 1 | 1 | 0 |
其中 1 表示这个元素在集合里存在。
得到这样的矩阵之后呢,接下来的一步就是将矩阵行进行打乱,随机排序
| Element | A | B | C | D |
|---|---|---|---|---|
| c | 0 | 1 | 0 | 0 |
| a | 1 | 0 | 1 | 1 |
| e | 0 | 1 | 1 | 0 |
| d | 0 | 1 | 1 | 1 |
| b | 1 | 0 | 0 | 1 |
在完全随机打乱的情况下,我们就可以得到每个集合的 MinHash 值,它等于每一列第一个值为1的行数。
于是,$h(A) = 1$, $h(B) = 0$, $h(C) = 1$, $h(D) = 1$ (这里从0开始数)
接下来最神奇的现象就发生了,两个集合 MinHash 值相等的概率等于这两个集合的 Jaccard 相似度
Proof
对于任意两个集合,S1 和 S2 来说,这两列所在的行只有三种可能:
- S1 和 S2 的值都为 1
- S1 和 S2 其中有一个的值为 1
- S1 和 S2 的值都为 0
第一种可能意味着 S1 与 S2 有一个共同的元素。
第二种可能则意味着有元素在 S1 与 S2 其中任意一个中,但不在所有。
第三种则意味着此元素在 S1 与 S2 中都不会出现。
我们设:
$x = |S1 \cap S2|$
$y = |S1 \cup S2|$
则有
$Jaccard(S1, S2) = \frac{x}{y}$
对于一个打乱的行来说, $h(S1) = h(S2)$ 的情况意味着从上往下第一次碰到第一种可能之前不会碰到第二种可能。
于是 $h(S1) = h(S2)$ 的概率则为在一系列事件1和2的排序中事件1为开头的可能性(事件3在这种情况下可以被忽略,因为我们只考虑1和2的排列组合)。
对于第一个元素,总共有 $y$ 个事件可以被放进去(并集的大小 $y$ 就等于交集的大小 $x$ 加上只有其中一个集合拥有的元素的数目),而其中事件 1 的个数为 $x$ (就是交集的大小,意味着都是共同的元素),则 $P(事件1在第一位) = \frac{x}{y} = Jaccard(S1, S2)$。得证。
MinHash Signature
通过上面的 MinHash 算法,我们可以从一个矩阵出发,得到多个打乱的矩阵,并且根据每个矩阵计算出 MinHash 值,由总尝试次数可以得出近似的概率。这个概率则近似与 Jaccard 相似度。
但是,聪明的会发现,这样算下来很麻烦,不仅得打乱好多次,每次新加入一个集合都需要新加入很多行和一列,非常的麻烦。我们可以选择再舍弃一些精确度,换来速度呢?
答案就是使用魔法最小哈希签名
最小哈希签名的基础概念是用哈希函数模拟打乱的过程
简单来说,就是建立一个新的矩阵,通过哈希函数,将原先的行转变成矩阵中的数字,极大的减小了计算量和存储空间。
具体的操作流程,其他人已经写的很详细了。
LSH (Locality Sensitive Hashing)
MinHash 签名已经能够帮助我们找出相似的集合,那么有没有办法再快一点点?
答案是有的,用 局部敏感Hash
通过分组的思想,将 MinHash 签名分为许多桶,在查找的时候首先找到相似的桶,再找到每个 MinHash 进行对比,速度理所当然会快很多。
通过分而治之的思想来用空间换时间,就是LSH搜索的精髓。
具体实现我也不讲了,反正最后我试验过了,决定不用这个东西。
已有算法的缺点
MinHash 和 LSH 归根结底依靠的是概率,所以它们的精确率(以及召回率)不是很高。至于实现的速度和空间利用,也没有达到我比较满意的程度。
我们可不可以跳出这个比较集合相似度的框架,来研究一些别的技巧?
最邻近搜索 Nearest Neighour Search
我们都知道,在空间中两个点之间的长度被称作它们的距离。两个点则分别可以用两个向量来表示,并且两个向量之间的距离可以计算出来。
这里有两种向量距离度量方式:
-
欧几里得度量 (Euclidean Distance)
对于 n 维空间的两点 p, q 来说,距离d
$d(p,q)={\sqrt {(p_{1}-q_{1})^{2}+(p_{2}-q_{2})^{2}+\cdots +(p_{i}-q_{i})^{2}+\cdots +(p_{n}-q_{n})^{2}}}$ -
余弦相似度 (Cosine similarity)
顾名思义,就是测量两个向量之间的夹角
$S_{C}(A,B):=\cos(\theta )={\mathbf {A} \cdot \mathbf {B} \over |\mathbf {A} |\mathbf {B} |}$
一般来说,我们最常用的距离度量方式还是欧几里得度量,可以考虑到所有维度上向量的信息。
还有,如果只看这两个公式的话会发现并没有解决我们的核心问题:速度。为了加快向量查询的速度,我们需要索引。
这里为了方便只介绍一个索引
HNSW(Hierarchical Navigable Small World)索引
如果你有一点图论基础的话,理解起来应该会很方便。
这个算法将N维空间中的向量构造成一张相互连通的图。
然而如果我们要细讲的话,首先得了解它的前身 NSW(Navigable Small World)索引。毕竟 HNSW 是在之上改进而成的。
在 NSW 中,作者使用了改进的 Delaunay Graph 算法。Delaunay Graph 保证没有任意一个顶点处于其他三角形外接圆的圆周上,由此来最大可能构造内角大的三角形。算法本身挺有意思,可以去看看(https://www.youtube.com/watch?v=GctAunEuHt4)。
为什么用 Delaunay Graph 来连接点?
- 不会出现孤点没有任何连接,导致无法被搜索到
- 相似的点互相连接,保证准确性
- 连接数量最少,提高效率
至于 NSW 采用了自己的高效 Delaunay Graph 算法:随机选取一个点然后找到与新插入的点最近的m个点,然后连接,that's it。
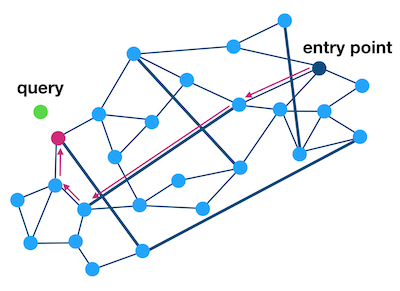
接下来,HNSW 则是多加了几层,提高了搜索效率,思想也是分而治之。

很显而易见,最底层 Layer 0 包含所有点,而越往上由指数衰减减少节点
搜索时候从上往下
详细的算法和推导,自己找吧
特征向量
那么这个和我们的推荐有什么用呢?
我们现在有一个输入值,这个输入值可能是文本,也可能是图片。
在经过一个特征提取函数 $f(x)$ 后,我们可以得到一个固定长度的向量,而这个向量,被称为特征。
特征的一个显而易见的特征就是它们越相似,通过度量算法得出来的距离越小。
现在基本都采用神经网络来提取特征值。
如果我们可以想办法,将任意大小的标签集合,转换为特征向量,这不就完美了?
HOT Encoder
采用和 MinHash 相似的计算方法,可以直接将向量的维度设置为总标签数量,对于每个标签集合,如果存在相应的标签则在向量中值对应设置为1。
这样可以直接想到,如果是两个标签集合生成的两个向量,存在相同的维度可以增加它们的相似性,符合我们的要求。
但是,缺点也显而易见。如果想要新增一个标签,则需要新增一个维度。数据库受不起这样的折腾的。
Word Embedding
嵌入(Embedding)即将别的特征转换为维度固定的特征向量。
摘抄一下Wiki: 词嵌入(Word embedding)是自然语言处理(NLP)中语言模型与表征学习技术的统称。概念上而言,它是指把一个维数为所有词的数量的高维空间嵌入到一个维数低得多的连续向量空间中,每个单词或词组被映射为实数域上的向量。
通过词嵌入的方式,我们可以将标签的语义考虑在内,并且生成独特的特征向量。
这是一个词神经网络需要做的事情。
首先,产生词向量的神经网络通过无监督学习对文本的特征进行学习。通过大量数据的输入,不管是采用词袋模型还是别的,都可以构造出一个词空间。在这个词空间内,每个不同的词都占据一个点。相似的词占据的点会更接近。
这就给了我们一些很有利的条件。
- 两个即使表现不同但是语义相似的词,可以被临近匹配。
- 多个词在集合里,如果我们想要取得整个集合的特征,直接计算每个词的特征,然后再经过向量的平均就可以了。
如果说这样很难懂的话,我画几张图来展示一下就好了吧
经过大量的学习,神经网络决定把 Apple 和 Pineapple 和 Pen 映射到一个二维空间内
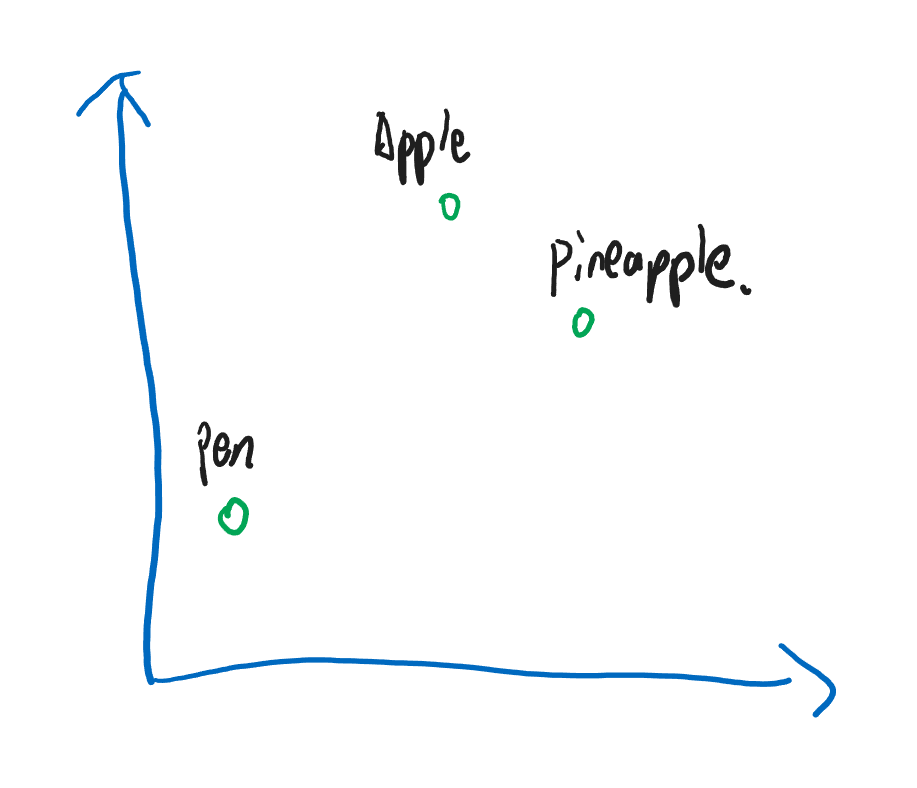
很理想的情况下,Apple 和 Pineapple 应该是离得很近,而 Pen 与它们的语义差太远了。
那么这时候,我们看一下,我想要知道 Apple 的推荐是什么,就应该计算一下它们之间的距离
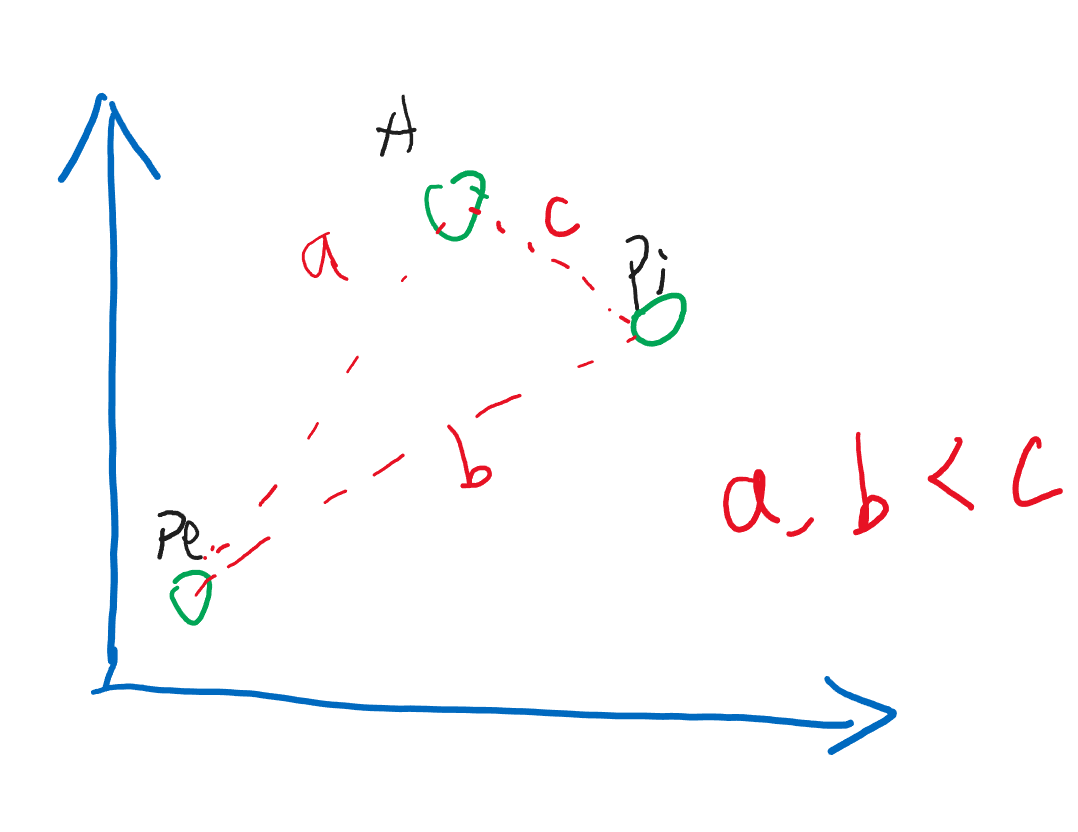
这时,两个语义相近的点会更接近,从而给 Pineapple 更高的分数,所以首先推荐 Pineapple
那么第二点的话,也可以通过图像来解释
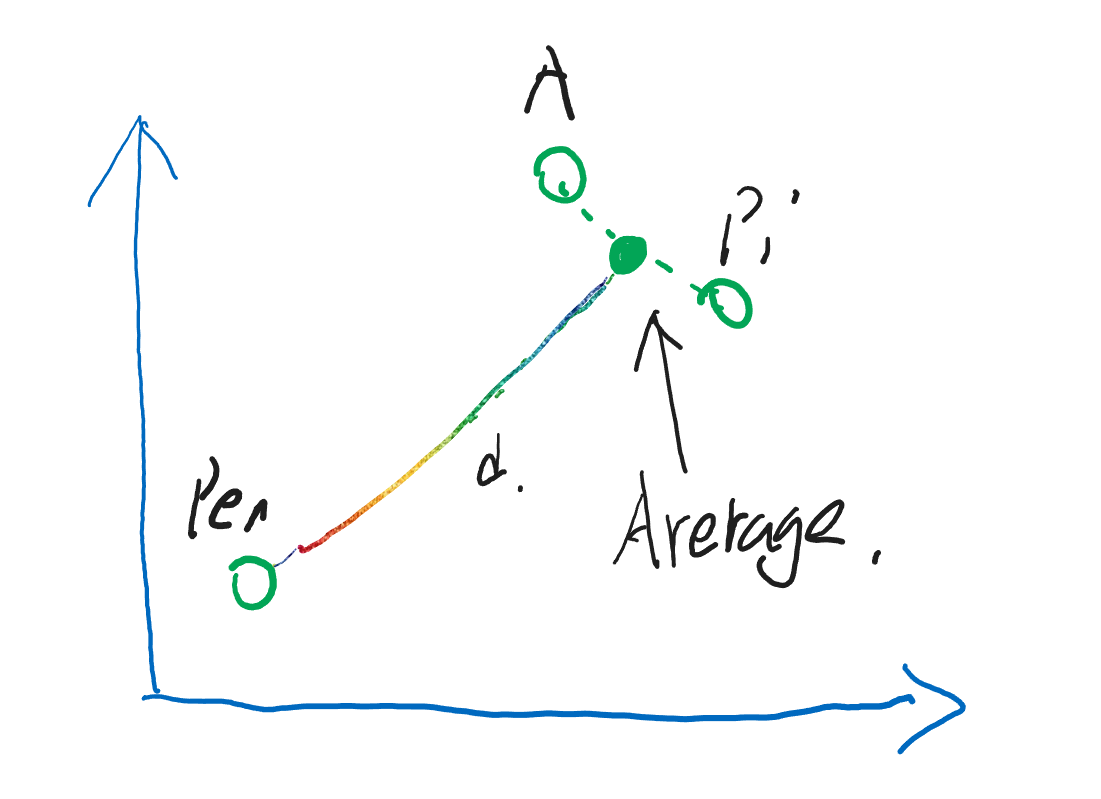
如果一个标签有 Apple 也有 Pineapple ,那正好,它们的中间离它们的距离相同,就意味着中间的点其实是融合了它们所有语义的点。
接下来,给这个标签推荐的内容,首先会和 Apple 和 Pineapple 很接近,其次才是 Pen 。
正是这种模型有用的性质,给了我新的启发。
神经网络+最邻近搜索
接下来,我们可以利用这两个的结合体,构造一个完美的,时间空间线性的算法,它可以帮助我们选出最佳的推荐图片。
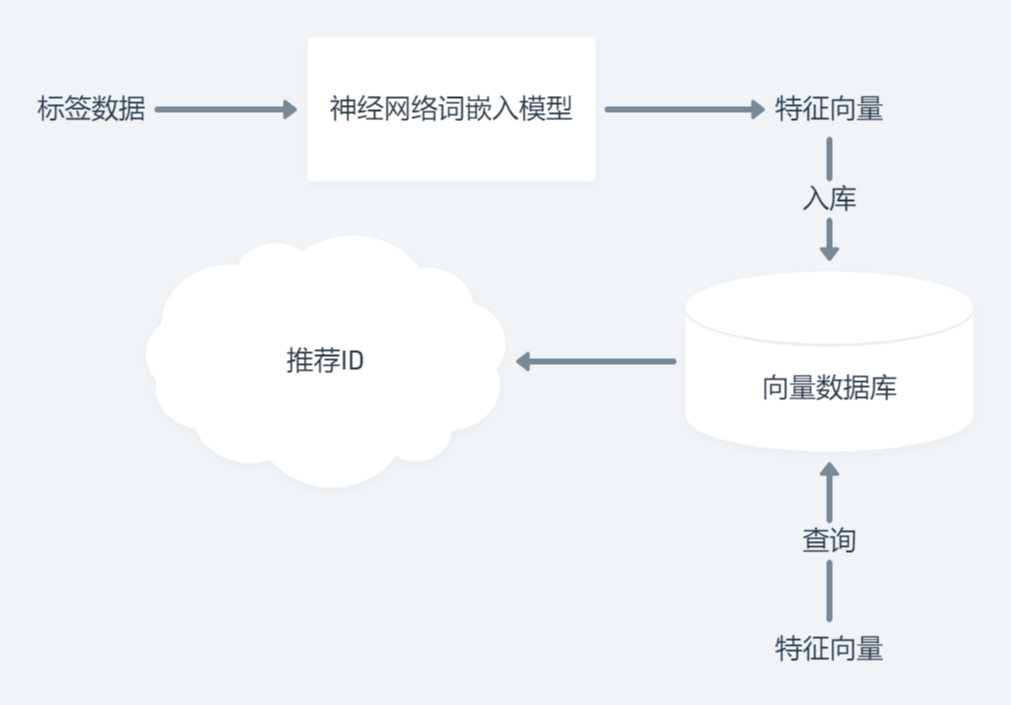
很有道理,但我当时不知道实践能不能用。于是事件出真知,我直接给它写到新版网站里,并且起个名叫做 NearDB
Over.
实践效果
由于我在开头提到了 Miku ,所以后面我们也得看一下 Miku
以千叶的一副画为例:
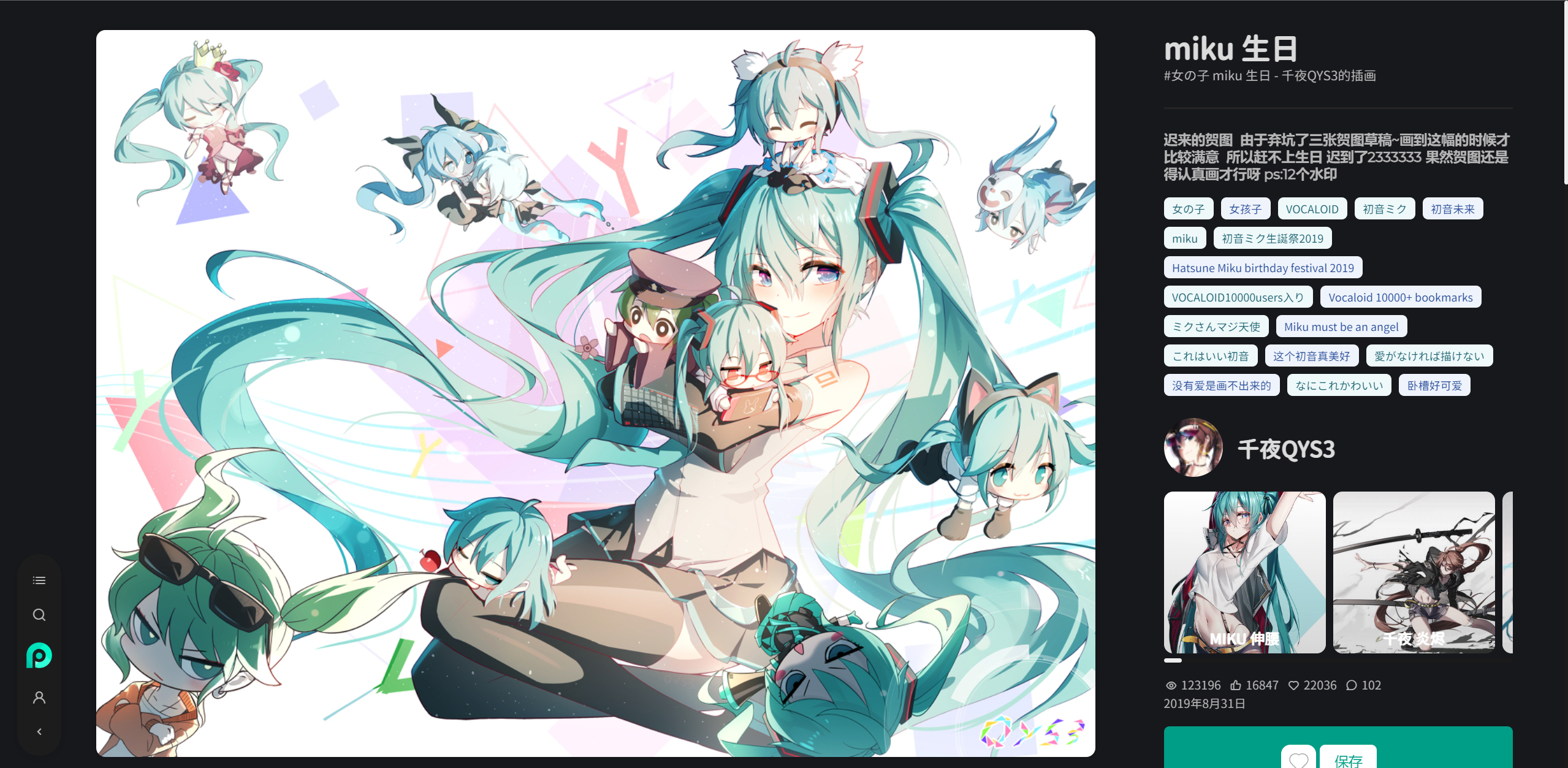
其中包含几个重要的标签:[女の子, VOCALOID, 初音ミク]
那么往下滑~~

清一色的 Miku 都在推荐中!
说真滴我第一次尝试之后都被效果震惊到了 hhh
改进措施?
由于前几天推荐服务器又崩掉了,一气之下直接动用钞能力整了太 4c4g 的服务器专门跑神经网络。
在迁移期间把之前没有了结的心愿实现咯,就是对于推荐,同时参考图片的“热门度”来排序。
这个问题呢,不能通过返回的列表再重新排序,因为那样子太慢了。我们需要让标签的相似度和热门度最高,通过放到一起实现快速的高质量推荐。
接下来回顾向量搜索的特征,不难发现,每一个维度的长度都是被考虑在欧几里得度量中的。
所以,不妨将热门度作为一个新的维度放在数据库里,搜索时候按照最大热门度去搜索
但是在具体实践上,因为距离只有0和无穷大,我们只能用0来表示最大的热门度,自然,新增的热门度维度只能是 $\frac{1}{热门度}$。
不过,效果还是太棒了,我太牛逼了吧
结尾
如果你正在设计一个小站的推荐系统,这篇文章将会提供一个很好的解决方案。
如果是大站的话,还是得从用户反馈入手,设立推荐系统。
这篇文章是我至今为止在博客写过最长的一篇,没有之一。其中融合了多个知识点,包括向量搜索,神经网络,以及集合相似度判断。这些都是在数据科学中很有用的工具,同时在软件工程中也是很有帮助。善用工具,工具也会助你一臂之力。

